a summary: We explain the signatures of Lamport, which is a safe, HASH digital signing scheme that relies on the retail developed in 1979. We use it to clarify how safe quantum safe signatures can be very simple and do not require complexity or new mathematics. We confirm that retail signatures may be the way to go, if Bitcoin is adopting a safe signing scheme. There is no concrete reason for the belief that quantum computing poses an imminent or medium -term threat to Bitcoin. However, from our point of view, the first step in alleviating the quantum risks visible gives users to choose bitcoin spending in a safe quantitative way. Once this choice is available, the extent to which the economic user can pay any steps the following.
American mathematics world and computer world Leslie Lambor
summary
Bitcoin’s quantitative risk is a hot theme today. There was even a conversation conference In San Francisco, in Presidio Bitcoin, dedicated to this issue. In our opinion, one must try to be as rational as possible. We do not understand quantum computing and have not seen any amounts that already achieve anything in particular, and therefore may not be worth anxious. However, we appreciate that the idea is frightening for some and that the development in quantum technology can theory to take place at an unexpected speed. One of the general concerns is that Bitcoin may need an update to a very new quantitative signing signing scheme. There are a lot of new luxury plans that one can read, including Hookand SQIand Falcon and Crystals. There may be risks associated with new plans; What if we choose the wrong plan, in 2023 it was there Reports That a new postpartum scheme, “Sick algorithmIt was broken through the non -classic method of non -ridicule.
However, if Bitcoin wants to upgrade to the post -quarter signing scheme, we do not necessarily need a sophisticated technology that is ever risky. Remember that the Bitcoin digital signature scheme, the digital signing of the ECDSA, is likely to be vulnerable to the quantity, due to a worker attack using Shore algorithm. Retail functions however, they are largely safe. Retail functions, such as Sha256, are exposed to quantity based on Grover algorithmWhich means that security can be reduced by the square root. So instead of 256 bits of security, there will be 128 bits of security. This looks mostly good and one can always use a retail function with greater output to increase safety if necessary.
There are already significant signing plans that depend on retail functions. For example Lamborbit signaturesIt was developed in 1979. This scheme is actually very simple, and much more simple than the elliptical curve -based scheme used by Bitcoin. And because it depends only on retail functions, it is a safe quantum. Therefore, if Bitcoin adds a quantum signing scheme, it does not need to rely on the new risky mathematics, we can only choose a retail -based scheme instead. Then Bitcoin can use retail functions for everything, prove mining for work and signatures, which makes Bitcoin simpler. In the rest of this report, we look at Lamborbit’s signatures and how it works.
How do Lamborbit signatures work?
In the following example, we assume that the signatures of Lamport uses the shame of Sha256, however it can work with any largely fragmented algorithm. With Lamport signatures, the private key is not just a random number of 256 -bit as it is with ECDSA, instead two sets of random numbers 256, 256 bit. The two groups are appointed A and B to our example. Therefore, the private key is 2 * 256 * 256 = 131,072 bits = 16.3 KB. Then each of these random numbers is 512 256 bits and this output is divided by the public key, so the public key is also 16.3 kb. The Bitcoin address can then be a shaft Sha256 of the sequence of all the strings that make up the public key. The photos below show the special and public key.
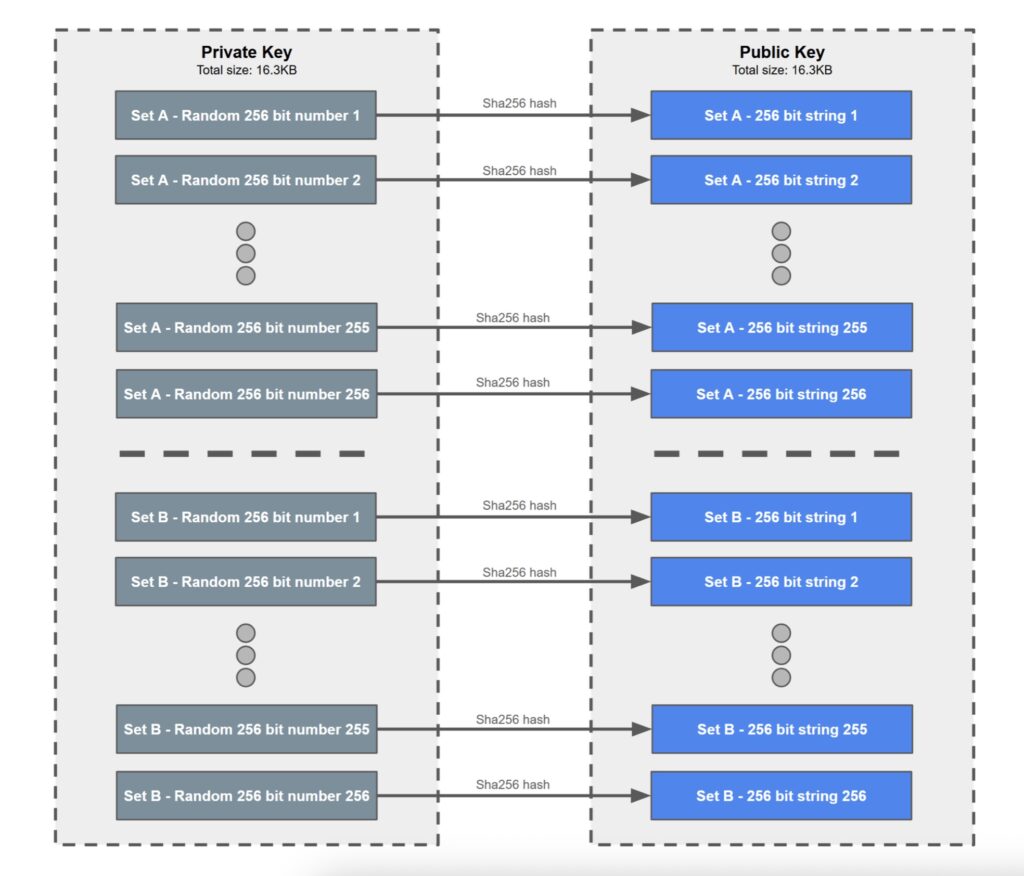
To sign a message, the first step is to divide the message, again using the Sha256 and the output chain is produced in the dualism. Based on each number of dual output, this is part of the private key in the signature. The value of a little zero corresponds to the A group A, while the value of one interest corresponds to the B. Therefore, the signature consists of a random group of exactly 50 % of the total private key.
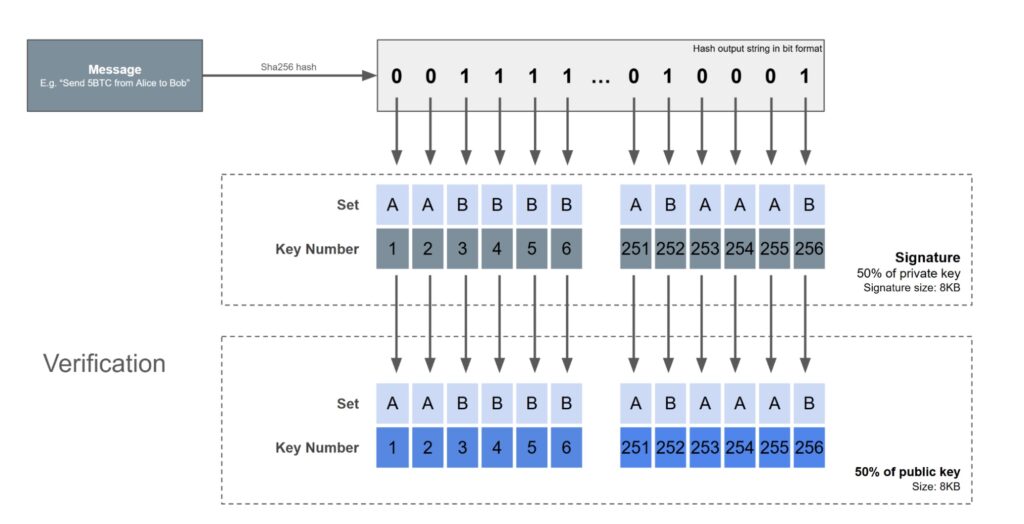
To check the message, all that is to verify is to divide the message and determine the appropriate parts of the public key using the same methodology. Then the auditor needs to divide each of the numbers in the signature, to see if they match these 256 parts of the public key. If there is a full match, the signature is valid. The site needed to know the full private key, given that the retail function is random and one cannot predict the parts of Group A or Set B, until a specific message was chosen. So it is relatively easy to see how this scheme is safe and also checking straightly forward.
Only once
Among the main weakness in this scheme is that it is limited to using each signature only once. Once the transaction is signed on Blockchain, 50 % of the private key is deployed. If the signature is used again, another 50 % of the key is deployed. Statistically, this means that 75 % of the total private key is now expected to be available to the public. It is easy to see how security deteriorates very quickly every time one signs. This means that people may not be able to reuse addresses, which is positive for privacy, but there are some problems here:
- People are used to reuse the addresses
- What if someone sent money to a title that has already been used?
- How will RBF work? There can be an additional additional input and not only an additional input can be signed, but this creates currency control problems
No smart mathematics
Another drawback is that one cannot do smart mathematics like one can do with ECDSA. BIP-32, for example, hierarchical inevitable wallets, take advantage of ECDSA properties to allow the use of “Xpubs”, which can only work with fragmentation.
measuring
Another elephant in the room is the huge size of public signatures and keys. With the signing of 8 kg and a public key is 16 km, this is a total of 24 kb. Bitcoin block cannot then include dozens of transactions, instead of thousands of transactions we have today. However, it appears that all quantum secure plans have this problem somewhat or another.
Astage muscle+
We only analyze the original basic Lamport signing scheme for illustrative purposes only, to show how the simple signature scheme that depends only on retail and therefore it is very safe. If Bitcoin will add a retail signature scheme, there are more modern options available. In 1982, Winternitz Publishing contrast in the Lamport chart. The Winternitz chart guarantees division division into a number of pieces and drawing these pieces to different parts of the private key; Then there are more repetitive retail steps. In 2011, the latest alternative XMSS It was published and then in 2015, another variable of the retail signing plan was published, Sphincter.
Astage muscle+ It can allow the sizes of smaller signature and special switches that can be used several times. These charts include the Merkle tree structure, where the upper part of the tree is “a global public key”, so the public key is only 32 bytes. If Bitcoin depends on a post -quarter signing scheme, these are retail schemes with Merkle trees that can be chosen. Since Merkle trees are already widely used in Bitcoin, they can be considered convenient to use here as well.
The co -founder of Lightning Lab, Olaoluwa Osuntokun recently on the signers+ at the last quantum conference in San Francisco. In the conversation, he explained how there are many bares that one can choose with the sphincter+, allowing us to achieve the required characteristics that we want depending on our priorities. Parameters that can be modified include the cost of retail to create signatures, the cost of retail to verify signatures, the quantity of safe reuse and the size of the signatures. Olaoluwa said that parameters can be set so that the signatures can be small at 2 km, which seems somewhat reasonable. Nevertheless, this of course is still much larger than the current signatures in Bitcoin, which can be about 70 bytes.
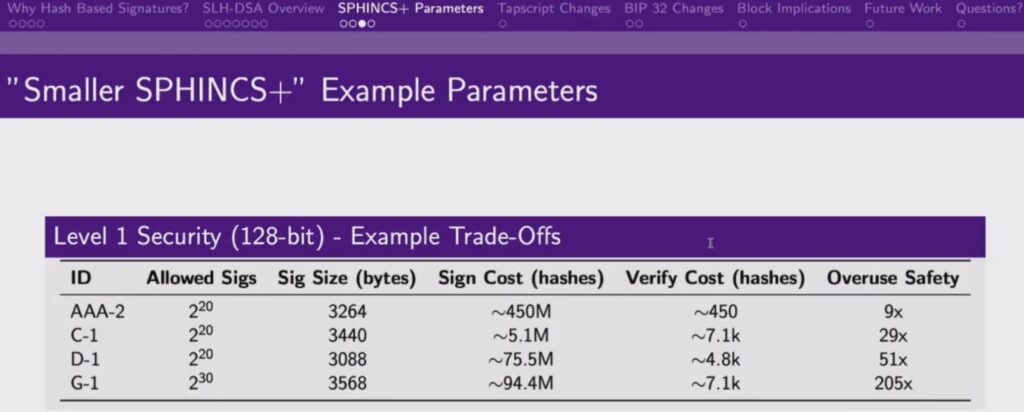
source: https://x.com/presidiBitcoin/status/1945877820657508650
conclusion
We do not have a strong understanding of the level of quantum risks on ECDSA and we have nothing tangible. From our point of view, it is very likely to be the ECDSA chart that Bitcoin uses safe for the next decades and the rational approach may be not to do anything until we have more concrete examples of quantum computers. However, it may be useful to think about what it takes to make bitcoin safe. The first step is to create a way to eliminate Bitcoin in a safe quantitative way, which can be a retail signature scheme. From our point of view, there are no significant points that discuss any plan to freeze weak coins so that the option of a safe and safe spending is available and widely used. If a safe quantum method is added to bitcoin spending and a strong user adoption, then only then deserves to participate in such a discussion.
Of course, there are many problems that must be worked on when it comes to adding a retail signature. If a new safe signing scheme is added that depends on HASH, how will we get adopting in view of the significant signature sizes, because these transactions are much more expensive? Do we re -visit the blocking discount and unit of the blocks? Instead, we can target economic adoption at value instead of adopting according to the transaction/UTXO number. These quantum secure plans may be adopted first by entities that retain thousands of bitcoin, such as etf or bitcoin wardrobe companies, which barely do any transactions. For these entities, the cost of additional treatment will not be great. Individual users can keep their savings in quantum safe outputs that require 2KB signatures, while daily spending may be weak. Spending on this day can be made to the day relatively safe using P2WPkh outputs and avoid re -use the address, if desired. Again using retail as quantum defense, with users only in danger while the treatment is unconfirmed.
Once there is a large economic dependence, it may be easier to talk about the following steps that must be tolerated in quantum risks. From our point of view, as soon as there is a quantum safe recovery option, economic users should eventually lead the path forward. If they do not use quantum safe outputs, then there is nothing wrong, this is their choice. If adoption is strong, we can move to talking about other controversial steps, such as frozen coins, change the maximum weight, or the Bip-39 phrase consisting of quantum safe recovery or any steps that one believes is necessary. Let the pregnant women decide.